Einführung¶

Es wird die Dynamik eines sphärischen Magnetpendels betrachtet. Das Modell hierzu besteht aus folgenden Teilen:

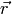Ein masseloser Faden der Länge $L$ ist im Koordinatenursprung befestigt. Daran hängt ein punktförmiger, ferromagnetischer Pendelkörper der Masse $m$ . Der Ort des Pendels ist durch $\vec{r}$ gegeben.
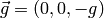
Auf die Pendelmasse wirkt die Schwerkraft: $V_\mathrm{P} = -m \vec{g} \vec{r}$ mit $\vec{g} = (0, 0, -g)$
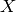An Orten $\vec{r}_i$ sind $N$ Magnete befestigt. Das Potential der Magnete ist gegeben durch $V_\mathrm{M} = -\sum_{i=1}^{N} \frac{\alpha_i}{|\vec{r}-\vec{r}_i|^X}$ , $X$ ist hierbei der Potentialexponent und 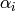$\alpha_i$ die Stärke des Magneten.

Die Bewegungsgleichungen werden mittels des Lagrange-Formulismus aufgestellt. Dabei werden Kugelkoordinaten verwendet. Die Reibung wird separat betrachtet und zu den gewonnenen Gleichungen addiert: $F_{F,\theta} = -m \gamma L \dot{\theta}$ und $F_{F,\phi} = -m \gamma L \sin \theta \dot{\phi}$ .

Um die Bewegungsgleichungen einheitenlos zu machen, werden folgende charakteristischen Größen definiert:

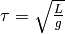
Zeit: $\tau = \sqrt{\frac{L}{g}}$
Magnetstärke: $\alpha_0 = m g L^{X+1}$
Reibung: $\gamma_0 = \frac{1}{\tau}$

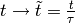Mit $t \rightarrow \tilde{t} = \frac{t}{\tau}$ , $\alpha_i \rightarrow \tilde{\alpha}_i = \frac{\alpha_i}{\alpha_0}$ , $\gamma \rightarrow \tilde{\gamma} = \frac{\gamma}{\gamma_0}$ erhält man einheitenlose Bewegungsgleichungen:

$\ddot\theta = \sin\theta -\tilde{\gamma} \dot{\theta} + \cos\theta \sin\theta\dot{\phi}^2 - \sum _{n=1}^N X \tilde{\alpha}_n \frac{\cos\theta \cos\phi\left(\cos\phi \sin\theta -\tilde{x}_n\right) + \cos\theta \sin\phi\left(\sin\theta \sin\phi-\tilde{y}_n\right) - \sin\theta\left(\cos\theta-\tilde{z}_n\right)}{\left(\left(\cos\phi\sin\theta-\tilde{x}_n\right)^2+\left(\sin\theta \sin\phi-\tilde{y}_n\right)^2 + \left(\cos\theta -\tilde{z}_n\right)^2\right)^{1+\frac{X}{2}}}$

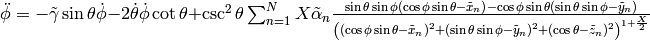
$\ddot{\phi} = -\tilde{\gamma } \sin\theta \dot{\phi} -2 \dot{\theta} \dot{\phi} \cot\theta +\csc^2 \theta \sum _{n=1}^N X \tilde{\alpha }_n \frac{\sin\theta \sin\phi \left(\cos\phi \sin\theta-\tilde{x}_n\right)-\cos\phi \sin\theta \left(\sin\theta \sin\phi-\tilde{y}_n\right)} {\left(\left(\cos\phi \sin\theta-\tilde{x}_n\right)^2+\left(\sin\theta \sin\phi-\tilde{y}_n\right)^2+\left(\cos\theta-\tilde{z}_n\right)^2\right)^{1+\frac{X}{2}}}$

Die Herleitung der Gleichungen findet sich auch im Mathematica-Notebook MagneticPendulum.nb.

Einführung¶

Vorheriges Thema

Nächstes Thema

Diese Seite

Navigation

Einführung¶

Vorheriges Thema

Nächstes Thema

Diese Seite

Schnellsuche

Navigation